The last set of hinge tests that I showed used a cut out a rectangle of material to form the links. By re-arranging a formula that calculates the required inter-link clearance, it’s possible to find the minimum number of links to make a bend using only a single cut with the laser if the width of the cut (laser kerf) is known. Its then also possible to calculate what the radius of that minimum bend is from the length of the lattice cut area.
For a 90 degree bend in a 3mm thick sheet and 3mm wide links, 23 torsional links are needed if the laser kerf is 0.2mm. This will form a bend with a 44mm internal radius.
Lattice Hinges
Lattice hinges are formed when a set of parallel, overlapping cuts divide a flat sheet into thinner, linked sections that can deform more easily than the solid sheet. By dividing the sheet into an array of parallel columns, each column can twist along its own length to let the sheet form a bend by twisting around the axis of these torsional links. Flexibility of the joint is determined by the material properties of the plate and the geometry (length of the overlapping cuts and cross sectional area) of the torsional links. For simplicity I’m only considering links where the width of the link is equal to the plate thickness.

Minimum Torsional Links
Laser kerf depends on the actual machine used for cutting, and is affected by a number of variables, including the laser’s focus adjustment, the speed of cutting and the type of material that is being cut, but it can be reasonably be assumed to be at least 0.2mm.
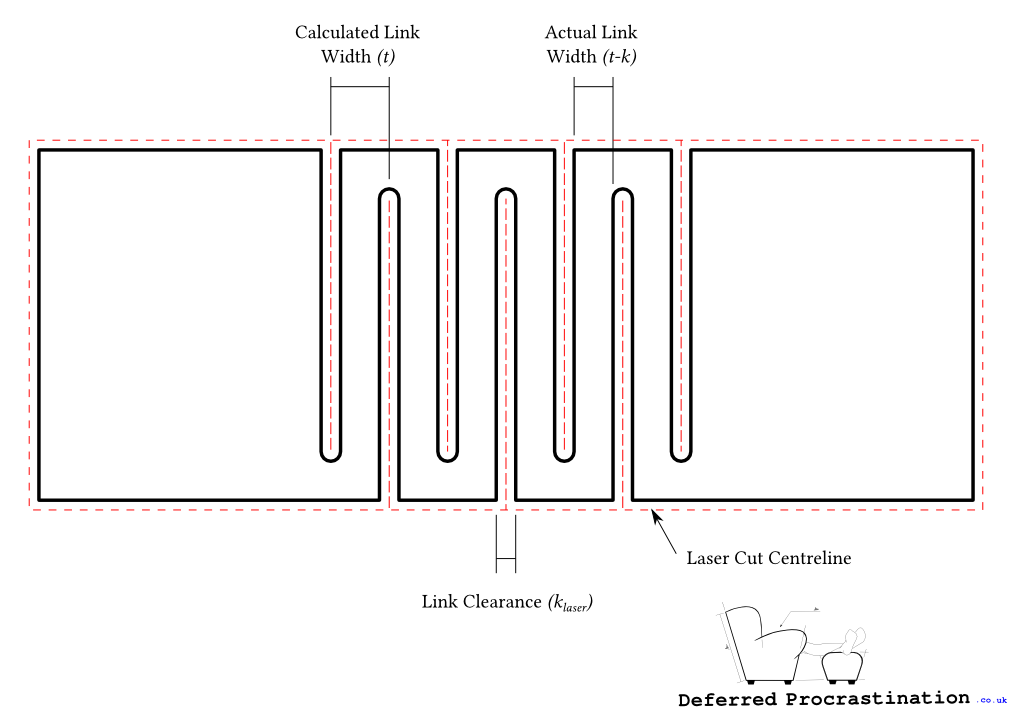
When the lattice hinge is bent, each torsional link twists along its length, and because the link has a rectangular cross section, the corners of the link will move into, and reduce the width of the gap between each link. As the size of each link is known and each link is assumed to be equal to the total bend angle divided by the number of links, its possible to calculate the required gap size so that the links do not touch in bending.

Link clearance k is given by:
$$ k = -t + 2 \sqrt{ \frac{t^2}{2} } \times \cos \left( \frac{\pi}{4} – \frac{\Theta}{n} \right) $$
so that can be rearranged to give the minimum value for the number of torsional links n where the clearance is less than or equal to the width of the laser kerf \(k_{laser}\):
$$ n \geq \frac{\Theta}{\frac{\pi}{4}-\cos^{-1}{\left( \frac{k_{laser} + t}{2 \sqrt{\frac{t^2}{2}}} \right)}} $$
For a 90 degree bend in 3mm material; \(n \geq 23\) links.
Bend Radius
If the minimum width of the bending lattice area is known, then it’s possible to calculate the radius of curve that this bend will form. And if you can calculate the bend radius, then it’s quite nice to be able to use that to give accurate support to each side of the bend for use in a structure.
I previously showed a formula for bend width that, while correct, is not exactly what I’ve been using since. While it’s possible to include the laser kerf when laying out the laser paths for cutting, that’s not what I’ve been doing in practice because it means including fractions of a millimeter. Instead, I’ve been assuming that the centreline dimensions of the cuts are the width of the links which, while not completely accurate because the laser removes a kerf width of material, is close enough to make the simplification useful.

If the distance between the laser cuts are set to equal to torsional link width t then the length of the lattice area, which is also the centreline arc length of the bend W is given by:
$$[ W = nt ]$$
From arc length, the inner and outer radii can be found:
$$[ r_{inner} = \frac{2W}{\Theta}-\frac{t}{2}]$$
$$[ r_{outer} = \frac{2W}{\Theta}+\frac{t}{2}]$$
This means that for a 90 degree bend in 3mm material with 23 links, it will form a bend where the inner radius is 44mm and the outer radius is 47mm.
Nomenclature
- \(k\) = Clearence gap (m)
- \(k_{laser}\) = Laser Kerf (m)
- \(l\) = Connected length (m)
- \(n\) = Number of columns of torsional links
- \(t\) = Material thickness (m)
- \(W\) = Total hinge Width (m)
- \(\Theta\) = Total bend angle of the piece (\(\Theta = \theta \times n\))
- \(\theta\) = Angle of twist per link (radians) (\(90° = \frac{\pi}{2}\) radians)